Structure of The Atom
The Sub-Atomic Particles:
The atom was regarded as the ultimate particle of matter according to Dalton’s Atomic Theory . It could explain various laws of chemical combination like the law of conservation of mass, the law of constant composition, and the law of multiple proportions satisfactorily . But it failed to explain the existence of sub-atomic particles like electrons and proton which were discovered later on.
Discovery of Electron:
Michael Faraday suggested the particle nature of electricity. As he passed electricity through a solution of an electrolyte, he found that chemical reactions occurred at the electrodes with the liberation and deposition of matter at the two electrodes.
Discovery of Electron—Discharge Tube Experiment :
In 1879 William Crooks studied electrical conduction with gas at very low pressure. The test was performed with a vacuum tube, a solid glass tube 60 inches long. As an example, it is closed at both ends and connected by two metal electrodes.
The Discharge Tube in the initial years :
The modern Discharge Tube :
Electrical discharge through gases can only be seen at very low pressures and at very high voltages.
The pressure of different gases can be changed to a desired value by evacuation. When a sufficiently high voltage is applied to the electrodes, current begins to flow as a beam of particles moving in the tube from the negative electrode (Cathode) to the positive electrode (Anode). They were called cathode rays or cathode ray particles.
• Characteristics of Cathode rays:
- The cathode rays move towards the anode starting from the cathode .
- The Cathode rays travel in straight lines.
- Cathode rays are made up of some material particles.
- Cathode rays produce a heating effect on metal surfaces they strike upon.
- They produce X-rays when they strike against the surface of the hard metals like Molybdenum, Tungsten, etc.
- On applying an electric field, these rays get deflected towards the positive plate. It shows that cathode rays carry a negative charge. These negatively charged particles are the Electrons.
- They produce green fluorescence when they strike crystals or plates of Zinc Sulphide.
- They possess a penetrating effect, they can penetrate very thin Aluminium foils..
- They can affect the photographic plates like the AgBr plates.
- They possess the same charge/mass ratio irrespective of the gas used in the discharge tube..
Hence , it could be concluded that electrons are the basic constituent of all atoms.
The extent of deviation of the particles from their path in the presence of an electrical or magnetic field solely depends upon
- the magnitude of the negative charge(s) on the particle- the greater the magnitude of the charge on the particle, the greater will be the deflection.
- the mass of the particle-lighter the particle, the larger is the deflection.
- the strength of the applied electrical or magnetic field.
Important features :
- The cathode rays move in a straight line.
- The cathode rays leave from the cathode and go towards the anode.
- These rays themselves are invisible, but their behavior can be observed using certain types of substances (fluorescent or phosphorescent) which glow when they hit them.
- Cathode rays consist of negatively charged particles. When an electric field is applied to the cathode rays using a pair of metal plates, they are deflected towards the positive plate, indicating the presence of a negative charge.
- The properties of cathode rays do not depend on the material of the electrodes and the nature of the gas in the cathode ray tube.
• Determination of the electron's charge-to-mass ratio (e/m)
J. J. Thomson was the first to experimentally determine the charge-to-mass ratio, called the e/m ratio for electrons. To do this, he exposed an electron beam emitted by a discharge tube with cathode rays to influence electric and magnetic fields. They run perpendicular to each other and for the path the electrons follow.
According to Thomson, the degree of deflection of particles in the presence of an electric and magnetic field depends on the following factors:
- The greater the charge on the particle, the greater is the interaction with the electric or magnetic field and hence, the greater is the deflection.
- Particle mass : the lighter the particle, the greater is the deflection.
- The deviation of the electrons from their original path increases/decreases with the increase/decrease of the voltage across the electrodes or the strength of the magnetic field.
Thomson was able to measure how much deviation the electrons notice in the strength of an electric field, or magnetic field to a greater accuracy and precision.
e/mₑ = 1.758820 x 10 ¹¹ C kg⁻¹ where mₑ = mass of electrons in kg
e = the amount of charge on the electron in terms of coulomb (C).
• Charging on Electrons
R A Millikan developed a method known as the Millikan's oil drop experiment to determine the charge of electrons.
• Discovery of Proton—Anode Rays
In 1886 Goldstein modified the discharge tube using a perforated cathode. As the pressure dropped, he saw a new type of light beam pass through a hole or bore in the cathode and move in the opposite direction of the cathode beam. These rays were called positive rays or bipolar rays or channel rays. The anode beams are not emitted from the anode, but from the space between the anode and the cathode.
• Anode Ray properties
- The amount of positive charge (e) of the particles forming the anode wire depends on the nature of the gas in the discharge pipe.
- The charge/mass ratio of 𝛼-particle depends on the gas in which it forms.
- A positively charged particle carries multiples of its elementary unit of charge.
- The behavior of these particles in a magnetic or electric field is opposite to that observed in electrons or cathode rays.
Characteristics of Positive rays/canal rays:
- The Anode-rays originate from the Anode and move towards Cathode.
- Anode rays consist of material particles.
- Anode rays are positively charged.
- The rays produce heat when they strike against a metallic surface.
- The magnitude of the charge on the rays varies from particle to particle depending upon the number of electrons lost .
- The mass of positive particles constituting these rays depend upon the nature of the gas used in the discharge tube.
- The charge/mass (or e/m) ratio of anode-rays is variable and it but depends upon the nature of gas used in the discharge tube. The value of e/m is greatest for the lightest gas, the Hydrogen.
The electric charge on the lightest positively charged particle from hydrogen gas was found to be exactly equal in magnitude but opposite in sign to that of an electron. So ,this lightest positively charged particle was named as a proton. The mass of a proton is almost 1836 times that of the electron.
As Hydrogen gas is taken inside the discharge tube
Charge on these particles = 1.6 × 10-19 coulomb
∴ Mass on each particle m =
This s nearly the same as that of the mass of a hydrogen atom.
•Protons
The smallest and lightest cations come from hydrogen and are called protons. mass of the proton = 1.6726 x 10⁻²⁷ kg
Charge on Proton e = (+) 1.602 x 10⁻¹⁹C
• Neutrons
The Neutron is a neutral particle. It was discovered by Chadwick in 1932 for which he was awarded the Noble Prize.
Bombardment of a thin sheet of beryllium with fast-moving alpha particles made him ascertained that the highly radiant rays consisted of neutral particles called neutrons.

Thomson's atomic model states that an atom is electrically neutral and consists of "small bodies" that act as negative ions. He also assumed that these negative ions or electrons moved in orbit to a shell with the same positive charge. This scientific model was compared to plum pudding, where the electron distribution is treated as a positively charged "plume" (raisin) called pudding. Therefore, the name Plum Pudding Model comes from Thomson's atomic model.
Functioning of Thomson’s Atomic Model
J.J. Thomson conducted a series of experiments to examine the nature of Cathode Rays. It was an attempt of him to conclude that Cathode Rays carried negative charge. The apparatus built by him was called the Cathode Ray Tube which is popularly known now a days as ‘Electron Gun’.
The figure below shows the Schematic representation of the same. Electrons emerging from the Cathode on the left end of the Tube travels through the slit (Anode), and comes in contact with the Phosphorescent screen at the right end of the Tube.
He found that the beam was deflected by the electric field while turning off the Magnetic field. He also could observed that by changing and adjusting the strengths of Electric and Magnetic field, the Cathode Rays did not deflect.
Fig. 3 – The Cathode Ray Tube Experiment for Thomson’s Atomic Model
At a low pressure of about 1 mm of Hg, the cathode ray appears slightly divergent and darkened near the cathode. This dark space expands through the tube at low pressure and appears blurry. When it hits glass or a phosphor screen, it emits light using the energy absorbed by the cathode rays. He measured the deflection, the length of the device, and the electric and magnetic field strengths to calculate the charge-to-mass ratio. He observed that this ratio was independent of the metal (charged plate) and the gas in the tube. These observations led him to conclude that these negatively charged particles were part of atoms.
He also observed that when a uniform magnetic field of strength B was applied perpendicular to the direction of motion of charged particles, the particles deflected in a circular path. The radius R of this circular path was obtained by setting the magnetic force ‘qvB’ equal to the centripetal force mv2/R. In his further experiments, Thomson used different amounts of electrical and Magnetic fields so as to keep the Cathode Ray beam straight without deflection. By equating the magnitudes of Electric and Magnetic forces, he could determine the speed of charged particle v.
According to Thomson,
- An Atom consisted of a positively charged sphere with electrons enclosed within it.
- Since the positive and negative charges are equal in magnitude, an Atom is electrically neutral.
- J.J. Thomson suggested that atoms can be thought of as spheres with a radius of about 10⁻¹º m, which are positively charged due to protons and have negatively charged electrons.
- In this model, the atom is visualized as a candy or cake with electrons embedded in it.
- According to this model, the mass of the atom is evenly distributed over the atom.
Applications of the Plum Pudding Model
- J. Thomson’s Cathode Ray experiment paved the way for the development of modern Electronics and could lay the foundation for the discoveries behind Transistors and Diodes.
- From these experiments, the Scientists found that Cathode Rays travel in a straight line which helped them to study the properties of Waves.
- Cathode Ray Tubes were developed (which are now popularly known as Electron Guns) and is widely used in many Electronic devices.
- His experiments led to a great revolution in Quantum Physics.
Drawbacks of Thomson's Atom Model
This model can explain the total neutrality of the atom, but it cannot satisfactorily explain the results of the scattering experiments performed by Rutherford in 1911.
Rutherford's 𝛼-particle scattering test
In 1911 Rutherford conducted several scattering experiments in which he bombarded metallic flakes such as gold, silver, platinum or copper with a beam of fast-moving 𝛼-particles. The thin gold foil had a circular fluorescent zinc sulfide plate. Every time 𝛼-particles hit the screen, a small flash of light was produced there.
He made the following observations of these experiments:
- Most of the 𝛼-particles passed through the foil without undergoing any deflection.
- A few 𝛼-particles underwent deflection through small angles.
- And Very few were deflected back making an angle of nearly 180°.
- Since most of the 𝛼-particles passed through the foil without undergoing any deflection, there must be sufficient empty space within the atom.
- A small fraction of 𝛼-particles was deflected by small angles. The positive charge must be concentrated in a very small volume that repelled and deflected a few positively charged 𝛼-particles. This very small and compact portion of the atom was called nucleus.
- The volume of nucleus must be very small as compared to total volume of atom.
- The positive charge and most of the mass of the atom are highly concentrated in an extremely small region which was named as nucleus by Rutherford.
- The nucleus is surrounded by electrons moving with a very high speed in circular paths around the nucleus , called orbits.
- Electrons and nucleus are held together by strong electrostatic forces of attraction.
• Atomic Number
- The atomic number (z) is the number of protons present in the nucleus .
For example, the number of protons in the Carbon nucleus is 6, in Magnesium atom it is 12, therefore, their atomic numbers are 6 and 12.
- Atoms are electrically neutral, so the number of electrons in an atom is equal to the number of protons or atomic number z.
For example, number of electrons in Carbon atom and Magnesium atom are 6 and 12 respectively.
Hence,
- Atomic Number (Z) = Number of protons in the nucleus of atom.
• Mass Number
- It is the total number of nucleons present in the nucleus of an atom and is called the Mass number (A) of the atom.
- Number of protons and neutrons present in the nucleus are known as nucleons.
- The total number of nucleons contribute to mass number (A) of the atom.
- It is the Sum of the protons and neutrons of an atom.
- Mass Number = Number of protons + Number of neutrons .
- Mathematically, A = p + n.
Isotopes of Hydrogen:
These three isotopes are shown in the figure below:
Isotopes of Chlorine :
There are two isotopes of Chlorine with mass numbers 35 and 37.
The two isotopes differ in their number of neutrons with 18 and 20 neutrons respectively.
Isotopes of Some Common Elements:
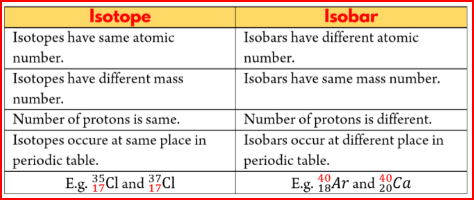
Characteristics of Isotopes
- As the isotopes of an element have the same Atomic number, but different Mass number, in the nuclei of isotopes there are same number of protons, but different number of neutrons.
- As the isotopes differ in their atomic masses, all the mass dependent properties of the isotopes are different.
- Since, the chemical properties are determined by the number of protons in the nucleus, and the number of electrons in the atom, chemical properties exhibited by the different isotopes of an element are similar .
- For example, all the isotopes of carbon burn in air to give carbon dioxide.
• Drawbacks of Rutherford's Atom Model
- When a body moves in an orbit, it has an acceleration. Thus, an electron with a negative charge on it and moving around nucleus in an orbit is accelerated.
Thus, Rutherford’s model was unable to explain the stability of atom when the motion of electrons was described on the basis of classical mechanics and electromagnetic theory.
- Rutherford’s model does not give any proper idea about distribution of electrons around the nucleus and about their energies.
There were two developments which had a major role in the formulation of Bohr’s model of atom. Those were:
- Dual character of the electromagnetic radiation which means that radiations possess both wave like and particle like properties.
- Experimental results regarding atomic spectra which could be explained only by assuming quantized electronic energy levels in atoms.
• Nature of Electromagnetic Radiation : Electromagnetic Wave Theory
The main postulates of the theory put forward by James Clark Maxwell in 1864 are as follows:
- The energy which is emitted from any source (like the heated rod or the filament of a bulb through which electric current is passed) continuously in the form of radiations is called the radiant energy.
- The radiations consist of electric and magnetic fields that oscillate perpendicular to each other and are both perpendicular to the direction of propagation of the radiation.
- The radiations possess wave character and they travel with the velocity of light, 3 x 108 m/s.
- These waves do not require any kind of material medium for propagation. For example, rays from the Sun reach us through space which is a not a material medium.
- Wavelength: It is defined as the distance between any two consecutive crests or troughs for a transverse wave or between any two consecutive compressions and Rarefactions for a longitudinal wave. It is represented by 𝝀 and its S.I. unit is metre.
- Frequency: Frequency of a wave is defined as the number of waves passing through any point in one second. It is represented by 𝜈 (nu) and is expressed in Hertz (Hz).
- Velocity: Velocity of a wave is defined as the linear displacement of the wave in one second.
- Amplitude: Amplitude of a wave is the height of the crest or the depth of the through in case of a transverse wave.. It is represented by A and is expressed in the units of length.
- Wave Number: It is defined as the number of waves present in a unit length of 1 metre . So, it is equal to the reciprocal of the wavelength.
Electromagnetic Spectrum:
Electromagnetic wave theory was successful in explaining the optical properties like reflection, refraction, dispersion, diffraction, interference, etc., but it could not explain the following phenomena:
- The phenomenon of black body radiation.
- The photoelectric effect.
- Variation of the heat capacity of solids as a function of temperature.
- The line spectra of atoms with reference to Hydrogen atom.
- The ideal body, which either emits or absorbs all frequencies is called a black body. The radiation emitted by such a body is known as black body radiation.
- For the emitted radiation from a black body, the exact frequency distribution depends only on its temperature.
- Intensity of radiation emitted at a given temperature, increases with decrease of wavelength, reaches a maximum value at a given wavelength and then keeps on decreasing with further decrease of wavelength.
This theory was further extended by Albert Einstein in the year 1905. Some of the main postulates of this theory are as follows:
- The radiant energy are absorbed or emitted in the form of small packets of energy. Each of those small packets of energy is called a quantum.
- The Energy of a quantum is directly proportional to the frequency of the radiation.
-
where h is the proportionality constant, known as Planck’s constant.
In the year 1887,Hertz, discovered that electrons are emitted or ejected from the metal surface when a beam of light of certain frequency strikes the surface of some metals . This phenomenon is known as photoelectric effect.
The Observations on Photoelectric Effect :
- The photons of light of certain minimum frequency called threshold frequency ( v0), can cause the photoelectric effect. v0 has different value for different metals.
- The kinetic energy of the electrons emitted is directly proportional to the frequency of the striking photons and is completely independent of their intensity.
- The number of electrons ejected per second from the metal surface depends upon the intensity of the striking photons or radiations and not on their frequency.
Explanation of the Photoelectric Effect
In the year 1905 Einstein gave an explanation of the different postulates of the photoelectric effect using Planck’s quantum theory as follows:
- Photoelectrons are ejected only when the incident light has a certain minimum frequency ,called threshold frequency (v0)
- When the frequency of the incident light (v) is larger than the threshold frequency (v0), the excess energy ( hv – hv0) is imparted to the electron as kinetic energy.
- Kinetic Energy (K.E.) is the difference of the frequency of the incident radiation (v) and the threshold frequency (v0)
- K.E. of the ejected electron is given by the relation,
This is the expression for the energy of the emitted electron.
- When the intensity of light is increased, more electrons are ejected but the energies of the electrons remains constant..
• Dual Behaviour of Electromagnetic Radiations
Scientists came to the conclusion from the study of behaviour of light, that light and other electromagnetic radiations have dual nature.
- They have wave nature as well as particle nature.
- Whenever radiation interacts with matter as during reflection or refraction, it displays particle like properties unlike those wavelike properties which it exhibits when it propagates, during interference and diffraction .
- Microscopic particles like electrons also exhibit this property of wave-particle duality.
• Spectrum
- When a ray of white light is passed through a prism, the wave with a shorter wavelength bends more than the one with a longer wavelength.
- Ordinary white light consists of waves with all the wavelengths in the visible range. So array of white light disperses into a series of coloured bands, called spectrum.
- The light of red colour with longest wavelength is deviated the least while the violet light with the shortest wavelength is deviated the most.
Continuous Spectrum
- When a ray of white light is analyzed by passing through a prism it is observed that it splits up into seven different distinct bands of colours from violet to red (V I B G Y O R ).
- As these colours are continuous so that each of them merges into the next the spectrum is called a continuous spectrum.
Emission Spectra
- Emission Spectra is observed when the radiations emitted from a source are passed through a prism and then received on a photographic plate.
- Radiations can be emitted in a number of ways like:
- From the Sun or a glowing electric bulb.
- By passing an electric discharge through a gas at very low pressure.
- By heating a substance to a very high temperature.
Line Spectra
- This phenomena is about appearance of some specific coloured lines on a photographic plate when vapours of volatile substances are viewed through a spectroscope.
- When the vapours of some volatile substance analyzed with the help of a spectroscope after they are allowed to fall on the flame of a Bunsen burner , some specific coloured lines appear on the photographic plate which are different for different substances.
For example, Sodium(Na) or its salts emit yellow light while Potassium or its salts give out violet light.
Absorption Spectra
- White light passed through the vapours of a substance then strikes a prism, dark lines appear in the continuous spectrum.
- The dark lines indicate that the radiations corresponding to them are somehow absorbed by the substance from the white light.
- This type of spectrum is called absorption spectrum.
- Dark lines appear exactly at the same positions where the lines in the emission spectra appeared earlier.
Line Spectrum of Hydrogen
- When the emitted light after passage of electric discharge through Hydrogen gas enclosed in a discharge tube at very low pressure is analyzed by a spectroscope, the spectrum is found to consist of a large number of lines which are grouped into different series.
- This complete spectrum is known as hydrogen spectrum.
In the year 1890,Rydberg gave a simple theoretical equation for the calculation of wavelengths and wave numbers of spectral lines in the different series of Hydrogen spectrum. The equation is known as Rydberg formula or Rydberg equation.
This relation remains valid for Hydrogen atom only.
Here Rₕ = constant, called Rydberg constant for Hydrogen and n₁ , n₂ are integers (n₁ < n₂)
For any particular series, the value of n₁ is constant while that of n₂ changes.
For example,
For Lyman series, n1 = 1, n2 = 2, 3, 4, 5………..
For Balmer series, n1 = 2, n2 = 3, 4, 5, 6………..
For Paschen series, n1 = 3, n2 = 4, 5, 6, 7………..
For Brackett series, n1 = 4, n2 = 5, 6, 7, 8………..
For Pfund series, n1 = 5, n2 = 6, 7, 8, 9………..
Thus, by substituting the values of n1 and n2 in the above equation, wavelengths and wave number of different spectral lines can be calculated. When n1 = 3, the expression given above is called Paschen’s formula.
• Bohr’s Model of Atom
In the year 1913, Niels Bohr proposed a new model of atom on the basis of Planck’s Quantum Theory. The main postulates of this model are :
- The electrons in an atom, revolve around the nucleus in certain definite circular paths called orbits.
- Each orbit is associated with some definite energy and therefore these are known as Energy levels or Energy shells. These are numbered as 1, 2, 3, 4……….. or K, L, M, N…
- Only those energy orbits are permitted for the electron in which angular momentum of the electron is a whole number multiple of h/2𝝿
- Angular momentum of electron is given by m v r = n h/2𝝿 , where, n = 1, 2, 3, 4, 5...and,
m = mass of the electron,
v = tangential velocity of the revolving electron,
r = radius of the orbit,
h = Planck’s constant, where
n is an integer.
- As long as an electron is present in a particular orbit, it neither absorbs nor emits energy and hence, its energy remains constant.
- When energy is supplied to an electron, it absorbs Energy only in some fixed amounts as quanta and jumps into higher energy state away from the nucleus and is said to remain in excited state.
- The excited state is unstable, the electron may return to the lower energy state by jumping back .
- In doing so, it would emit the same amount of energy. (∆E = E2 – E1).
- Bohr’s theory could explain the stability of an atom.
- Bohr’s theory could help in calculating the energy of electron in hydrogen atom and other species.
- The mathematical expression for the energy of an electron in the nth orbit is given by,
- Bohr’s theory could explain the atomic spectrum of hydrogen atom.
• The Limitations of Bohr’s Model
- The theory failed to explain the atomic spectra of the atoms containing more than one electron or multi-electron atoms.
- Bohr's theory could not explain the fine structure of the spectral lines.
- Bohr’s theory failed to offer any satisfactory explanation of Zeeman effect and Stark effect.
- Bohr’s theory could not explain the ability of atoms to form molecule formed by chemical bonds.
- It could not comply with the Heisenberg’s uncertainty principle.
• Dual Behaviour of Matter : de Broglie Equation
In the year 1924, de Broglie proposed that matter, like radiation, should also exhibit dual behaviour -It should exhibit both particle like and wave like properties. This means that like photons, electrons must have momentum as well as wavelength.• Heisenberg’s Uncertainty Principle :
Heisenberg’s Uncertainty Principle states that, “It is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron”.
- It rules out existence of definite paths or trajectories of electrons and other similar particles.
- The effect of Heisenberg’s uncertainty principle is significant only for microscopic objects and is negligible for macroscopic objects.
• Reasons for the Failure of Bohr Model
- The wave character of the electron is not considered in Bohr Model.
- According to Bohr Model an orbit is a clearly defined path and this path can completely be defined only if both the position and the velocity of the electron are known exactly at the same time.
- This is not possible according to the Heisenberg’s uncertainty principle.
• Quantum Mechanical Model of Atom
Quantum mechanics: Quantum mechanics is a theoretical science that deals with the study of the motions of the microscopic objects that have both observable duality or wave like and particle like properties.
Some Important Features
- Quantization: The Energy of electrons in atom is quantized i.e., can only have certain values.
- Duality : The existence of quantized electronic energy level is a direct result of the wave like properties of electrons.
- Uncertainty : Both the exact position and exact velocity of an electron in an atom can not be determined simultaneously.
- Orbital wave function φ : An atomic orbital has wave function φ. There are many orbitals in an atom. Electron occupy an atomic orbital which has definite energy. An orbital cannot have more than two electrons. The orbitals are filled in increasing order of energy. All the information about the electron in an atom is stored in orbital wave function φ.
- Probability density : The probability of finding electron at a point within an atom is proportional to square of orbital wave function i.e., |φ2|at that point. It is known as probability density and is always positive.
- Most probable region : From the value of φ2 at different points within atom, it is possible to predict the most probable region around the nucleus where electron will be found.
• Quantum Numbers
- Atomic orbitals can be specified using their corresponding Energies and angular momenta which are quantized. ( they have specific values).
- The quantized values can be expressed in terms of quantum numbers n, l, m, s.
- These numbers are used to fetch complete information about an electron i.e., its location, energy, spin etc.
- They can also be used to get a sketch of the shapes of different orbitals.
The most important quantum number , n is the Principal Quantum number which describes the principal energy level or shell to which the electron belongs. It is denoted by the letter n and can have any integral value except zero, i.e., n = 1, 2, 3, 4……….. etc.
The Principal energy shells are designated by the letters, K, L, M, N, O, P ….. etc. starting from the nucleus.
The principal quantum number gives us the following information:
- It can give the average distance of the electron from the nucleus.
- It determines the energy of the electron completely in hydrogen atom and hydrogen like particles.
- Using Hund's Rule, the maximum number of electrons present in any principal shell is given by 2n2 where n is the number of the principal shell.
Azimuthal or Orbital Angular or Subsidiary Quantum Number (ℓ)
This number helps to explain the fine lines of the spectrum which are present in addition to the spectra of the elements containing the main lines.
The azimuthal quantum number can give the following information:
- The number of subshells like s, p, d, f present in the main shell.
- The angular momentum(L= m r 𝟂) of the electron present in any subshell.
- The relative Energies of various subshells or orbitals.
- The shapes of the various orbitals or subshells present within the same principal shell.
- This quantum number is denoted by the letter ℓ. For a given value of n, it can have any value ranging from 0 to (n – 1). For example,
For the 2nd shell (L), n = 2, the possible value of ℓ can be 0 and 1.
- Subshells that correspond to different values of ℓ are represented by the following symbols:
Notation for subshell s p d f g h ………………..
Magnetic Orbital Quantum Number (m )
- The magnetic quantum number is denoted by letter m and for a given value of ℓ, it can have all the values ranging from – ℓ to + ℓ including zero.
- For the 1st shell, n=1, so ℓ=1-1=0,
- For energy value of ℓ, m has 2ℓ + 1 values.
For ℓ = 0 (K- shell or s-subshell), m can have only one value. i.e., m = 2ℓ + 1 =2(0)+1=1.
- In other words, K- shell has only one orbital called s-orbital.
- Atoms in K-Shell have their electronic configuration
- Their electronic configuration is shown as
- When n=2, ℓ =1, So, For energy value of ℓ = 1, m has 2ℓ + 1 =2(1)+1=3 values. For example,
- In other words, L-shell has only two orbitals called s-orbital with 1 orientation and p-orbital with 3 orientations in space.
- Atoms in L-Shell have their electronic configuration
- Their electronic configuration is shown as
For ℓ = 1 (L-shell and p-subshell), m can have only three values. Here, m = -1, 0, +1 .
So p-subshell has only three orientations in space.
- Similarly, When n=3, ℓ =2, So, For energy value of ℓ = 2, m has 2ℓ + 1 =2(2)+1=5 values. For example,
- In other words, M-shell has three orbitals called s-orbital with 1 orientation , p-orbital with 3 orientations and d-orbital with 5 orientations in space.
- Atoms in M-Shell have their electronic configuration
- Their electronic configuration is shown as
For ℓ = 2 (L-shell and p-subshell), m can have only five values. Here, m = -2, -1, 0, +1, +2 .
So d-subshell can have five orientations in space.
- Lastly, When n=4, ℓ =3, So, For energy value of ℓ = 3, m has 2ℓ + 1 =2(3)+1=7 values. For example,
- In other words, N-shell has four orbitals called s-orbital with 1 orientation , p-orbital with 3 orientations , d-orbital with 5 orientations and f-orbital with 7 orientations in space.
- Atoms in N-Shell have their electronic configuration
- Their electronic configuration is shown as
For ℓ = 3 (N-shell and f-subshell), m can have seven values. Here, m = -3, -2, -1, 0 , +1, +2, +3 .
So f-subshell can have seven orientations in space.
- This quantum number is helpful to to explain the magnetic properties of the substances.
- It bases on the fact that a spinning electron behaves like a micromagnet with a definite magnetic moment.
- The two magnetic moments oppose and cancel each other, if an orbital contains two electrons.
- The two kind of rotations are clockwise (↓) and anticlockwise (↑), represented by a pair of vertical arrows(↑) and (↓).
- Their graphical representation is as follows:
- s - orbital
Use of Quantum Numbers (Tabular View)
• Shapes of s-orbitals
- s-orbital is in the s-subshell. For this subshell, ℓ = 0 and m = 1. Thus, s-orbital with only one orientation will have a spherical shape with uniform electron density along all the three axes.
- The probability of 1s electron is found to be maximum near the nucleus and decreases with the increase in the distance from the nucleus.
- In 2s electron, the probability is also maximum near the nucleus and decreases to zero probability gradually outwards.
- The Spherical empty shell for 2s electron is called nodal surface or simply a node.
- An s-orbital is not directional in nature, it can not influence the shape of a molecule.
• Shapes of p-orbitals
- p-orbitals are present in the p-subshell for which ℓ = 1 and m can have three possible orientations – 1, 0, + 1.
- Hence, there are three orbitals in the p-subshell which are designated as px, py and pz orbitals depending upon the axis along which they are directed.
- The general shape of a p-orbital is dumb-bell consisting of the two portions called lobes.
- In addition, there is a plane passing through the nucleus along which finding of the electron density is almost zero. This is known as the nodal plane.
- From these dumb-bell figures, it is obvious that unlike s-orbital, a p-orbital is also directional in nature.
- Hence p-orbital influences the shapes of the molecules in the formation of which it participates.
• Shapes of d-orbitals
- For d-orbitals or d-subshell, ℓ = 2, m can have five possible orientations – -2, -1, 0, 1, 2.This means that there are five orientations leading to five different orbitals.
- These are represented by dxy, dyz, dzx, dx2-y2 and dz²; for example, 3dxy, 3dyz, 3dzx, 3dx²-y² and 3dz².
- The dxy, dyz, and dzx orbitals have the same shape ( cloverleaf shape) but they lie in XY, YZ, and ZX planes respectively.
- Hence, there are five d-orbitals.
- These different orbitals have different orientations.
- The dz² orbital is symmetrical about Z-axis . It has a dumbbell shape with a doughnut-shaped electron cloud in the centre.
- The dx²-y² orbital is also clover leaf-shaped . But its leaves are directed along the X and Y-axis.
- The reason for the presence of four lobes in any d orbital is justified by the fact that the d – orbitals have two nodes. So there are two changes in algebraic sign of ψ, which lead to four lobes.
- The d orbitals have two angular nodes (it means two angles at which the probability of electron is always zero).
- There is a set of five d orbitals (with complicated shapes and names) as well as the 3s and 3p orbitals (3p ₓ , 3py, 3pz).
- At the third level, there is a total of nine orbitals in all.
- The magnetic orbital quantum number for d orbitals m is given as ( -2, -1, 0, 1, 2 ).
- Out of these five d orbitals, shapes of the first four d-orbitals dxy, dyz, dzx, dx²-y² and dz² are interrelated , which is different from the dz² orbital whereas the energy of all five d orbitals is the same.
• Aufbau Principle
- Aufbau Principle states that " In the ground state of the atoms, the orbitals are always filled in order of their increasing energies."
- In other words, electrons prefer to occupy the lowest energy orbital available to them and enter into the higher energy orbitals only when the lower energy orbitals are filled.
- Following is the order in which the energies of the orbitals increase and hence the order in which the orbitals are filled :
- The order may be remembered by using the method given in figure above.
• Pauli Exclusion Principle
- According to this principle, "No two electrons in an atom can have exactly the same set of four quantum numbers."
- It can also be stated as: "The two electrons which may exist in the same orbital must have opposite spins".
• The Hund’s Rule of Maximum Multiplicity
It states that: "Pairing of electrons in the orbitals that belong to the same subshell (p, d or f) would not take place until each of the orbitals belonging to that subshell has got one electron each" i.e., it is singly occupied.
• The Electronic Configuration of Atoms
Electronic configuration is the distribution of electrons into orbitals of an atom. The electronic configuration of different atoms can be represented in these two ways.For example:
Example of finding Electronic configuration of an element:
And the electronic configuration of Germanium is written as
• Stability of the Completely Filled and the Half Filled Subshells
The stability of completely filled and half filled subshells is due to the following reasons:
- The stabilizing effect arises whenever two or more electrons with same spin are present in the degenerate orbitals of a subshell. These electrons tend to interchange their positions.
- The energy released due to this exchange is called exchange energy.
- When the subshell is either half filled or completely filled, the number of exchanges that can takes place is maximum.
- As a result the exchange energy is maximum and so is the stability of the subshell.
In the following article we shall study and discuss some of the most important problems in Classification of Elements and Periodicity in Properties which are of utmost importance for the annual and Entrance examinations like NEET, JEE, IIT etc.
Thanks for reading the article till the end.
Bye.
For Personal guidance and coaching,
- For Joining



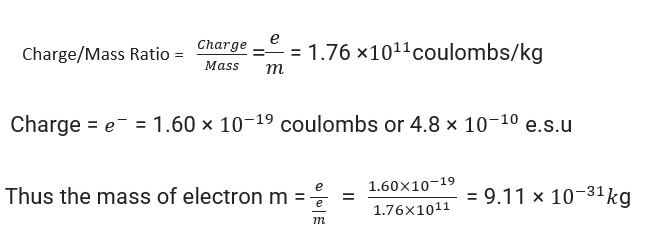






















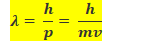































No comments:
Post a Comment