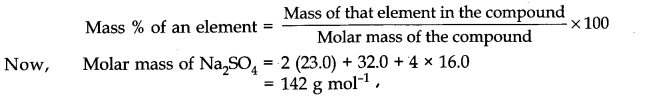Class 11 Chapter 1(b): Basics of Chemistry: Concentration Units by Subhas C Chakra

 

What  is Concentration ?

Concentration is the degree to which one substance is present in a mixture. The concentration of each substance in a mixture can be expressed in mass or volume units. The components of the mixture can be gases, liquids, or solids.

Concentration and Mixtures :

Concentration is a ratio of how much of one ingredient is present in a mixture, compared to the whole mixture or compared to the main ingredient, often the solvent. The amounts of each substance can be expressed in mass or volume units, and many different units can be used. The components of the mixture can be gases, liquids, or solids.

• Earth’s atmosphere, for example, is a mixture of gases, and 78% of the total volume is nitrogen gas.   In other words, the concentration of nitrogen in Earth’s atmosphere is 78%.
•  Different types of steel are mixtures of iron with other elements. For example, stainless steel has close to 20%, by weight, of chromium. 
• Sometimes a combination of mass and volume measurements are used; vinegar can be said to be a 5% solution of acetic acid, meaning 5 g of acetic acid per 100 mL of solution.
• Concentration also refers to the process of removing solvent from a solution to increase the proportion of solute. 
• The Dead Sea becomes more concentrated in salts as water evaporates from the surface
•  Ores are produced by the concentration of valuable minerals , such as those containing gold or silver, in small region of Earth's crust.

 As  it is not usually practical to analyze the whole body of substance in question,  only samples are taken.  

More About Concentration:

Concentration, as a verb, refers to the process of removing solvent from a solution to increase the proportion of solute. Concentration of a salt solution is achieved, for example, by allowing water to evaporate from the solution.

Some facts about the concentration Units :

• For example, the concentration of nitrogen in the atmosphere changes slightly with altitude; sampling only at sea level would not be sufficient to characterize the whole atmosphere.
• Many commonly used mixtures are liquid solutions. 
• For chemical reactions, Molarity is one of the most useful unit of concentration.
•  Molarity  is the number of moles of solute per liter of solution.
•  Concentrated hydrochloric acid is 12 M, meaning that there are 12 moles of hydrogen chloride per liter of water solution. 
• Other useful units of concentrations are Molality, Normality  and mole fraction and ppm or parts per million.
• Molality is  the number of moles of solute per kilogram of solvent.
• Normality  is the number of chemical equivalents or gram equivalents per liter of solution.
• Mole fraction  is the ratio of the numbers of moles of solute and solution. 
• PPM  or parts per million is used when very small amounts of a substance are present,  sometimes  parts per billion is also  used.
• A sample of tap water may contain 35 parts per million of dissolved solids.
• Exposure levels of dust or vapors in air may be given in units of mass of substance per volume of air.
• The maximum acceptable level for human exposure to ammonia vapor, for example, is 27 mg per cubic meter of air for short term exposure, that is, during a 15-minute period.
• Because modern analytical instruments require only small samples, results are often reported in milligrams per milliliter or nanograms per milliliter. 
• Clinical laboratory reports of substances in blood or urine may be reported as milligrams per deciliter.

 Measurement of Concentration :

• Concentration is the quantity of dissolved substance per unit quantity of solvent in a solution. Concentration is measured in various ways. 
• The Strength of a solution is the amount of Solute ( in terms of  mass or volume) found in unit amount of Solution ( in terms of  mass or volume). 
• The amount of substance dissolved per unit volume (symbol c) has units of mol dm⁻³ or mol l⁻¹. 
•  The mass concentration (symbol ρ) is the mass of solute per unit volume of solvent. 
• It has units of kg dm⁻³, g cm⁻³, etc. 
• The molal concentration or molality ( symbol m) is the amount of substance per unit mass of solvent, commonly given in units of mol kg⁻¹.

Method of Calculating Concentration:

(a) Strength (S) of a Solution:

The Strength of a solution is the ratio of the amount of solute (Mass/Volume) present in an amount of Solution (Mass/Volume).

Since both solute and solution can be measured in terms of mass and volume, there may be four different concentration units.

Calculation of Strength

(b) Percentage (P) of a Solution :

The Percentage concentration of a solution is calculated by multiplying its strength with 100%.

Percentage (P) = Strength x 100%

(c)   Molarity (M) of a Solution :

• To calculate the molarity of a solution, the number of moles of solute must be divided by the total liters of solution produced. 
• If the amount of solute is given in grams,  calculate the number of moles of solute using the solute’s molar mass.  
• Then calculate  the molarity  using the number of moles and total volume.

 Molarity (M),   is the number of moles of solute per liter of solution. 

This molar concentration (c_i) is calculated by dividing the moles of solute (n_i ) by the total volume (V) of the solution., where n_i is the number of moles of solute present in V litre of the solution

${\text{c}}_{\text{i}}=\frac{{\text{n}}_{\text{i}}}{\text{V}}$

$$ci=niV

• The SI unit for molar concentration is mol/m³. 
• However, mol/L is a more common unit for molarity. 
• A solution that contains 1 mole of solute per 1 liter of solution (1 mol/L) is called “one Molar” or 1 M. 
• The unit mol/L can be converted to mol/m³ using the following equation:

          1 mol/L = 1 mol/dm³ = 1 mol dm⁻³ = 1 M = 1000 mol/m³

Calculating Molarity Given Moles and Volume

 What is the molarity of this solution If   11.7 grams of NaCl are dissolved in water to produce a 2.0 L of solution,?

• First, we have to  convert the mass of the solute NaCl in grams into moles. 
• We do this by dividing  the mass of solute by its molecular Mass  (58.5 g/mole).

$11.7\text{grams NaCl}\times \frac{\text{1 mole}}{58.5\text{g/mole}}=0.2\text{moles NaCl}$

• Then, we divide the number of moles by the total solution volume to get concentration.

${\text{c}}_{\text{i}}=\frac{{\text{n}}_{\text{i}}}{\text{V}}$

${\text{⇒c}}_{\text{i}}=\frac{0.2\text{moles NaCl}}{2\text{liters solution}}$

${\text{⇒ c}}_{\text{i}}=0.1\text{M}$

The NaCl solution is a 0.1 M solution.

Calculating Moles Given Molarity

To calculate the number of moles in a solution given the molarity, we multiply the molarity by total volume of the solution in liters.

How many moles of potassium chloride (KCl) are in 4.0 L of a 0.65 M solution?

${\text{1 L of solution contains 0.65 moles of potassium chloride (KCl)⇒ 4 L of solution contains 0.65 x 4= 2.60 moles of potassium chloride (KCl)Hence, there are 2.6 moles of KCl in a 0.65 M solution that occupies 4.0 L.Alternatively,}}^{}$

${\text{c =}}^{}\frac{{\text{n}}_{\text{i}}}{\text{V}}$

$\mathrm{\Rightarrow \; 0.65}\text{M}=\frac{{\text{n}}_{\text{i}}}{4.0\text{L}}$

$0.65\text{ M}=\frac{{\text{n}}_{\text{i}}}{4.0\text{ L}}$

${\text{n}}_{\text{i}}=\left(0.65\text{M}\right)\left(4.0\text{L}\right)=2.6\text{moles KCl}$

Hence, there are 2.6 moles of KCl in a 0.65 M solution that occupies 4.0 L.

Calculating Volume Given Molarity and Moles

We can also calculate the volume required to meet a specific mass in grams given the molarity of the solution. 

For example,
How many milliliters of a 4.0 M solution of NH₃-HCl are required to receive 51.0 g of NH₃?

• First we must convert grams of NH₃ to moles by dividing the mass by the molecular weight.

$\frac{51.0\text{g}{\text{NH}}_3}{17.0\text{g/mole}{\text{NH}}_3}=3.0\text{moles}{\text{NH}}_3$

Once we know our need to achieve 3.0 moles of NH_3, we can use this and the given molarity (4.0 M) to calculate the volume needed to reach 51.0 g.

${\text{Now that we know that there are 51.0 g of NH3 present in 0.75 L, we would need 750 mL of solution to obtain 51.0 g of NH3. (Ans)}}^{}$

Dilution

Dilution is the process of reducing the concentration of a solute in a solution, usually by adding more solvent. This relationship is represented by the equation c₁V₁ = c₂V₂, where c₁ and c₂ are the initial and final concentrations, and V₁ and V₂ are the initial and final volumes of the solution.

Example 1

A scientist has a 5.0 M solution of hydrochloric acid (HCl) and his new experiment requires 150.0 mL of 2.0 M HCl. How much water and how much 5.0 M HCl should the scientist use to make 150.0 mL of 2.0 M HCl?

We know that for any solution before and after its making,

c₁V₁ = c₂V_2, 

_Where,

• c₁ and V₁ are the concentration and the volume of the initial solution, which is the 5.0 M HCl. 
• c₂ and V₂ are the concentration and the volume of the desired solution, or 150.0 mL of the 2.0 M HCl solution. 
• The volume does not need to be converted to liters yet because both sides of the equation use mL. Hence,

$\left(5.0\text{M HCl}\right)\left({\text{V}}_1\right)=\left(2.0\text{M HCl}\right)\left(150.0\text{mL}\right)$

where, V₁ = 60.0 mL of 5.0 M HCl

• If 60.0 mL of 5.0 M HCl is used to make the desired solution, the amount of water needed to properly dilute the solution to the correct molarity and volume can be calculated:

Here, 150.0 mL – 60.0 mL = 90.0 mL

• So,  for the scientist to make 150.0 mL solution of  2.0 M HCl, he will need 60.0 mL of 5.0 M HCl and 90.0 mL of water.

Example 2

Water was added to 25 mL of an initial  solution of 5.0 M HBr until the total volume of the solution was 2.5 L. What is the molarity of the new solution?

• We are given the following:  c₁= 5.o M,  V₁= 0.025 L,  V₂= 2.50 L. 
• We are asked to find c₂, which is the molarity of the diluted solution.
• Now using the formula     c₁ V₂= c₂  V₂

(5.0 M)(0.025 L) = c₂ (2.50 L)

${\text{c}}_2=\frac{\left(5.0\text{M}\right)\left(0.025\text{L}\right)}{2.50\text{L}}=0.05\text{M}$

• Here, all of the units for volume have been converted to liters. 
• We calculate that we will have a 0.05 M solution,  if we diluted 25 mL of a concentrated solution to 2500 mL.

Molality

Molality is the concentration unit of a solution that gives the moles of solute present  per kilogram of the  solvent.

• Molality is a property of a solution and is defined as the number of moles of solute per kilogram of solvent.
• The SI unit for molality is mol/kg. A solution with a molality of 3 mol/kg is often described as “3 molal” or “3 m.” 

 Some important facts :

• Molality: The concentration of a substance in solution, expressed as the number of moles of solute per kilogram of solvent.
• Colligative property: A property of solutions that depends on the ratio of the number of solute particles to the number of solvent molecules in a solution, and not on the type of chemical species present.

• Intensive property: A property of matter that does not depend on the amount of matter.                                                                                                  
•   Measurements of Mass (Molality) vs. Volume (Molarity)

• Molality is an intensive property of solutions. 
•  Generally, it is calculated as the moles of a solute divided by the kilograms of the solvent. 
• Unlike molarity, which depends on the volume of the solution, molality depends only on the mass of the solvent. 
• Since volume is subject to variation due to temperature and pressure, molarity also varies by temperature and pressure. 
• Hence using weight is often an advantage as mass does not vary with ambient conditions. 
• We see molality being used while working with a range of temperatures.

Defining Molality

The molality,   m, of a solution is defined as the amount of  solute in moles,   ( n_solute), divided by the mass in kg of the solvent, ( m_solvent )  

${\text{m =}}^{}\frac{{\text{n}}_{\text{solute}}}{{\text{m}}_{\text{solvent}}}$

Molality is based on mass, so it can easily be converted into a mass ratio, denoted by m:

${\text{m(M}}_{\text{solute}})=\frac{{\text{n}}_{\text{solute}}}{{\text{m}}_{\text{solvent}}}=\frac{{\text{w}}_{\text{solute}}}{{\text{w}}_{\text{solvent}}}$

 In many weak aqueous solutions, the molarity and molality are similar as one kilogram of water (the solvent) occupies one liter of volume at room temperature, and the small amount of solute has little effect on the volume of the solvent.

A salt water solution: Table salt readily dissolves in water to form a solution. If the masses of the salt and of the water are known, the molality can be determined.

Units

The SI unit for molality is mol/kg, or moles of solute per kg of solvent. 

Calculating Molality

It is easy to calculate molality if we know the mass of solute and solvent in a solution. Molality is an intensive property, and is therefore independent of the amount being measured. This is true for all homogeneous solution concentrations.    The concentration or the molality remains constant,  regardless of the volume of the   sample of the same solution.  

Calculating Molality Given Mass

If we take   1.49 g of KCl and dissolve this   in 40 mL of water, what is the molality of the solution?    

• Remember that molality is moles of solute/kg per solvent. 
• KCl is the solute, while water is the solvent. 
• The molecular mass of KCl will be the sum of the molecular masses of K (39.0) and Cl (35.5 ).
•  It is 39.0 + 35.5 = 74.5
• We will have to calculate first  the amount of moles present in 1.49 g of KCl:

$\text{Moles of KCl}=1.49\text{g}\times \left(\frac{1\text{moles}}{74.5\text{g}}\right)=\mathrm{0.02 moles\; KCl}$

• We also need to convert the the 56.0 mL of water to its equivalent mass in grams by using the known density of water (1.0 g/mL):

$40.0\text{mL}\times \left(\frac{1.0\text{g}}{\text{mL}}\right)=40.0\text{g}$

• 40.0 g of water is equivalent to 0.040 kg of water. 
• Now, we can divide the moles of solute by the kg of solvent to find the molality of the solution:

$\text{Molality}=\left(\frac{\text{moles}}{\text{kg solvent}}\right)=\left(\frac{\mathrm{0.02 moles\; KCl}}{0.040\text{kg water}}\right)=0.5\text{m}$

The molality of  KCl and water solution is 0.5 m. Since the solution is very dilute, the molality is almost identical to the molarity of the solution, which is also 0.5 M. 

[We know that, Molarity = n/V =0.02 moles/0.040 L=0.02/0.04=1/2 M = 0.5 M]

Calculating Mass Given Molality

We can also use molality to find the amount of a substance in a solution.      

 For example,         

How much acetic acid, in mL, is needed to make a 3.0 m solution containing 39.0 g of KCN?

• First, we must convert the sample of KCN from grams to moles:

$\text{moles of KCN}=39.0\text{g}\times \left(\frac{1\text{moles}}{65.0\text{g}}\right)=0.6\text{moles}$

• The moles of KCN can then be used to find the kg of acetic acid. 
• We multiply the moles by the reciprocal of the given molality (3.0 moles/kg) so that our units appropriately cancel. 
• The result is the desired mass of acetic acid that we need to make our 3 m solution:

$0.6\text{moles KCl}\times \left(\frac{\text{kg acetic acid}}{3.0\text{moles KCl}}\right)=0.2\text{kg acetic acid}$

•  The mass of acetic acid in kg, is to be converted from kg to grams: 0.2 kg is equal to 200 g. 
• Next, we use the density of acetic acid (1.05 g/mL at 20 ^oC) to convert it to the requested volume in mL. 
• We must multiply by the reciprocal of the density to accomplish this:

$200.0\text{g acetic acid}\times \left(\frac{\text{mL}}{1.05\text{g}}\right)=190.476\text{mL acetic acid}$

Therefore, we require 190.5 mL of acetic acid to make a 3.0 m solution that contains 39.0 g of KCN.

Mole Fraction and Mole Percent

Mole fraction is the number of molecules of a given component in a mixture divided by the total number of moles in the mixture.

• Mole fraction describes the number of molecules (or moles) of one component divided by total the number of molecules (or moles) in the mixture.
• Mole fraction is useful when two reactive components are mixed together, as the ratio of the two components is known if the mole fraction of each is known.
• Multiplying mole fraction by 100 gives mole percent, which describes the same thing as mole fraction, just in a different form. Mole fractions can be generated from various concentrations including molality, molarity and mass percent compositions.

• Mole: The SI base unit for the amount of a substance; the amount of substance that contains as many elementary entities as there are atoms in 0.012 kg of carbon-12.
• Mole fraction: The ratio of the number of moles of one component in a mixture to the total number of moles.

Mole Fraction

In chemistry, the mole fraction, x_i, is defined as the amount of moles of a constituent, n_i, divided by the total amount of moles of all constituents in a mixture, n_tot:

${\text{x}}_{\text{i}}=\frac{{\text{n}}_{\text{i}}}{{\text{n}}_{\text{tot}}}$

Mole fractions are dimensionless, and the sum of all mole fractions in a given mixture is always equal to 1.

Characteristics of  Mole Fraction

The mole fraction is used very frequently in the construction of phase diagrams. It has a number of advantages:

• It is not temperature dependent, as opposed to molar concentration, and does not require knowledge of the densities of the phase(s) involved.
• A mixture of known mole fractions can be prepared by weighing the appropriate masses of the constituents.
• The measure is symmetric; in the mole fractions x=0.1 and x=0.9, the roles of ‘ solvent ‘ and ‘ solute ‘ are reversible.
• In a mixture of ideal gases, the mole fraction can be expressed as the ratio of partial pressure to total pressure of the mixture.

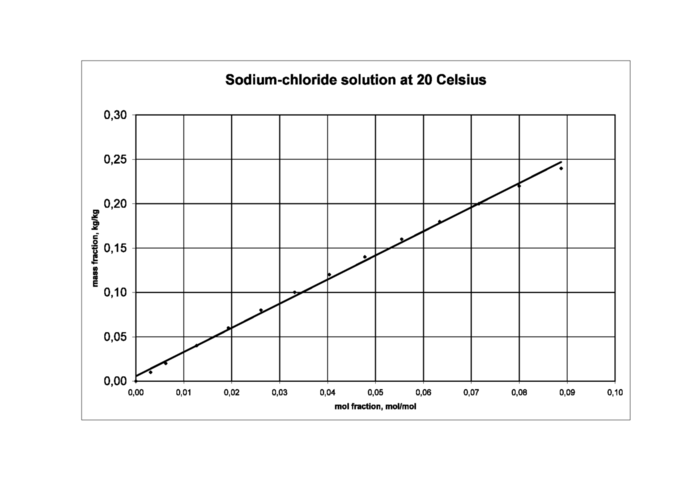
Mole fraction in a sodium chloride solution: Mole fraction increases proportionally to mass fraction in a solution of sodium chloride.

Mole Percent

• Multiplying the mole fraction by 100 gives the mole percentage, also referred as amount/amount percent (abbreviated as n/n%). 
•  All the mole per cents of a mixture add up to 100 mole percent. 
• We can easily convert mole percent back to mole fraction by dividing by 100. 
• A mole fraction of 0.60 is equal to a mole percent of 60.0%.

Calculations with Mole fraction and Mole Percent

Mole Fraction in Mixtures

A mixture of gases was formed by combining 6.4moles of O₂ and 5.6 moles of N₂. What is the mole fraction of each gas  in the mixture?

First, we must find the total number of moles with n_total = n_N₂ + n_O₂.

${\text{n}}_{\text{total}}=6.4\text{moles}+5.6\text{moles}=\text{12.0}\text{moles}$.

Next we must divide the moles of one of the component gases  N₂ by the total number of moles:

The mole fraction of nitrogen in the mixture is 0.47.

Hence mole fraction of Oxygen will be 1-0.47 = 0.53, which can be verified by dividing moles of Oxygen by the total number of moles in the gaseous mixture.

We have,

 

Mole Fraction in Solutions

Mole fraction can also be applied in the case of solutions. 
For example, 
0.1 moles of NaCl are dissolved in 100.0 mL of water. What is the mole fraction of NaCl?

• We are given the number of moles of NaCl present in  the volume of water. 
• First, we convert this volume to a mass by using the density of water (1.00 g/mL). 
•  Then we convert this mass to moles of water:

$100\text{mL}{H}_{2}O\times \left(\frac{1.0\text{g}}{1\text{mL}}\right)=100.0\text{g}{\text{H}}_2\text{O}=\; 100.0\; g\; x\left(\frac{1\text{moles}}{18.0g}\right)=5.55\text{moles}{\text{H}}_2\text{O}$

• With this information we can find the total number of moles present: 5.55 + 0.10  = 5.65 moles. 
• If we divide the moles of NaCl by the total number of moles, we find the mole fraction of this component:

$\text{x}=\left(\frac{0.10\text{moles}}{5.65\text{moles}}\right)=0.0176$

We find that the mole fraction of NaCl is 0.0176.

Mole Fraction with Multi-Component Mixtures

        Mole fractions can also be found for mixtures that  are formed  from multiple components.   Likewise the earlier cases, the total mole fraction of the mixture must be equal to 1.

For example,

A solution is formed by mixing 10.0 g of pentane (C₅H₁₂),  10.0 g of hexane (C₆H₁₄)  and  10.0 g of benzene (C₆H₆). What is the mole fraction of hexane in this mixture?

• We must first find the number of moles present in 10.0 g of each component, given their chemical formulas and molecular weights. 
• The number of moles for each is found by dividing its mass by its respective molecular weight. 
• We find that there are 0.138 moles of pentane, 0.116 moles of hexane, and 0.128 moles of benzene.
• We can find the total number of moles by taking the sum of all the moles: 0.138+0.116+0.128 = 0.382 total moles. 
• If we divide moles of hexane by the total moles, we calculate the mole fraction:

$\text{x}=\left(\frac{0.116\text{moles}}{0.382\text{moles}}\right)=0.303$

          Hence, the mole fraction for hexane is 0.303.

Mole Fraction from Molality

Mole fraction can also be calculated from molality. Example :

In a 1.62 m solution of table sugar (C₆H₁₂O₆) in water, what is the mole fraction of the table sugar?

• Since we are given molality, we can convert it to the equivalent mole fraction, which is already a mass ratio.
• We know that  molality = moles of solute/kg of  solvent. 
• Here we have a solution with 1.62 moles of sugar and 1.00 kg (1000 g) of water. 
• As the number of moles of sugar is known, now  we try  to find the moles of water using its molecular weight:

$1000\text{g}{\text{H}}_2\text{O}\times \left(\frac{1\text{mole}}{18.0\text{g}}\right)=55.5\text{moles}{\text{H}}_2\text{O}$

• The total number of moles is the sum of the moles of water and  sugar, which  is        55.5 +1.62 = 57.12 moles of solution. 
• We can now find the mole fraction of the sugar:

$\text{x}=\left(\frac{1.62\text{moles sugar}}{57.12\text{moles solution}}\right)=0.0284$

With the mole fraction of 0.0284, we see that we have a 2.84% solution of sugar in water.

Mole Fraction from Mass Percent

The mole fraction can also be calculated from a mass percent. 

What is the mole fraction of cinnamic acid that has a mass percent of 50.00% urea in cinnamic acid?

• The molecular weight of urea is 60.16 g/mol and the molecular weight of cinnamic acid is 148.16 g/mol.
• First, let us  assume a total mass of 100.0 g, which means that we have 50.0 g of urea and 50.0 g of cinnamic acid. 
• We can then calculate the moles present by dividing each by its molecular weight. 
• Thus, we have 0.833 moles urea and 0.388 moles cinnamic acid, so that we have 1.22 moles in total.
• To find the mole fraction, we divide the moles of cinnamic acid by total number of moles:

$\text{x}=\left(\frac{0.388\text{moles cinnamic acid}}{1.22\text{moles solution}}\right)=0.318$

• Hence, the mole fraction for cinnamic acid is 0.318.

In the following article we shall discuss some of the most important problems which are of utmost importance for the annual and Entrance examinations like NEET, JEE, IIT etc.

Thanks for reading the article till the end.  

Bye.